（本小题满分14分）已知函数
，其中
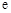为自然对数的底数．
（Ⅰ）求曲线
在点
处的切线方程；
（Ⅱ）若对任意
，不等式
恒成立，求实数
的取值范围；
（Ⅲ）试探究当
时，方程
解的个数，并说明理由．
x＋1的倾斜角的
，且分别满足下列条件的直线方程：(1)经过点(
，1＋
为空间四边形
的边
上的点，且
，求证：
.
中
，
面
，
，
面
.
相关知识点
推荐套卷
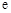（本小题满分14分）已知函数，其中为自然对数的底数．
（Ⅰ）求曲线在点处的切线方程；
（Ⅱ）若对任意，不等式恒成立，求实数的取值范围；
（Ⅲ）试探究当时，方程解的个数，并说明理由．
粤公网安备 44130202000953号