某涵洞是抛物线形,它的截面如图所示,现测得水面宽AB=1.6米,涵洞顶点O到水面的距离为2.4米,建立如图所示的直角坐标系.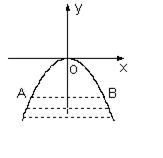
(1)试写出涵洞所在抛物线的解析式;
(2)当水面上涨了1.4米时,求水面的宽.
相关知识点
推荐套卷
某涵洞是抛物线形,它的截面如图所示,现测得水面宽AB=1.6米,涵洞顶点O到水面的距离为2.4米,建立如图所示的直角坐标系.
(1)试写出涵洞所在抛物线的解析式;
(2)当水面上涨了1.4米时,求水面的宽.