选修4-1：几何证明选讲（本小题满分10分）
如图，在△ABC和△ACD中，∠ACB＝∠ADC＝90°，∠BAC＝∠CAD，⊙O是以AB为直径的圆，DC的延长线与AB的延长线交于点E. 若EB＝6，EC＝6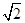
，求BC的长．
，求△AOB面积的最大值
在点
处的切线方程为
，求函数
的解析式；
平面SAP;
表示b；
的方程；
在
轴上截距的取值范围；
面积的最大值推荐套卷
选修4-1：几何证明选讲（本小题满分10分）
如图，在△ABC和△ACD中，∠ACB＝∠ADC＝90°，∠BAC＝∠CAD，⊙O是以AB为直径的圆，DC的延长线与AB的延长线交于点E. 若EB＝6，EC＝6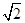，求BC的长．
粤公网安备 44130202000953号