设椭圆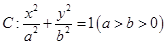 的左、右焦点分别为
的左、右焦点分别为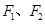 ,上顶点为
,上顶点为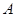 ,在
,在 轴负半轴上有一点
轴负半轴上有一点 ,满足
,满足 ,且
,且 .
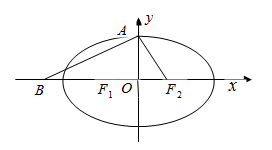
.
(1)求椭圆 的离心率;
的离心率;
(2)若过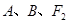 三点的圆与直线
三点的圆与直线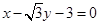 相切,求椭圆
相切,求椭圆 的方程;
的方程;
(3)在(2)的条件下,过右焦点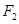 作斜率为
作斜率为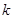 的直线
的直线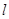 与椭圆
与椭圆 交于
交于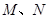 两点,线段
两点,线段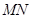 的中垂线与
的中垂线与 轴相交于
轴相交于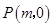 ,求实数
,求实数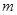 的取值范围.
的取值范围.
推荐套卷
设椭圆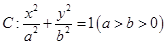 的左、右焦点分别为
的左、右焦点分别为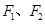 ,上顶点为
,上顶点为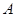 ,在
,在 轴负半轴上有一点
轴负半轴上有一点 ,满足
,满足 ,且
,且 .
.
(1)求椭圆 的离心率;
的离心率;
(2)若过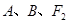 三点的圆与直线
三点的圆与直线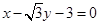 相切,求椭圆
相切,求椭圆 的方程;
的方程;
(3)在(2)的条件下,过右焦点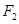 作斜率为
作斜率为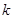 的直线
的直线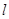 与椭圆
与椭圆 交于
交于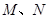 两点,线段
两点,线段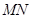 的中垂线与
的中垂线与 轴相交于
轴相交于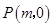 ,求实数
,求实数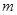 的取值范围.
的取值范围.