已知
的顶点A（0，1），AB边上的中线CD所在直线方程为
，AC边上的高BH所在直线方程为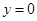
.
（1）求的项点B、C的坐标;
（2）若圆M经过不同的三点A、B、P（m、0），且斜率为1的直线与圆M相切于点P
求：圆M的方程.
，求不等式
的解集
Rl，其中R为扇形半径，l为弧长）
；
，试确定实数的取值范围
,求y关于t的函数关系式,t的范围.推荐套卷
已知的顶点A（0，1），AB边上的中线CD所在直线方程为，AC边上的高BH所在直线方程为.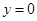
（1）求的项点B、C的坐标;
（2）若圆M经过不同的三点A、B、P（m、0），且斜率为1的直线与圆M相切于点P
求：圆M的方程.
粤公网安备 44130202000953号