某中学校本课程共开设了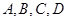
共
门选修课,每个学生必须且只能选修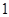
门选修课,现有该校的甲、乙、丙
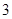名学生.
（Ⅰ）求这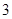名学生选修课所有选法的总数；
（Ⅱ）求恰有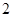
门选修课没有被这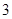名学生选择的概率；
（Ⅲ）求
选修课被这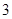名学生选择的人数
的分布列和数学期望.
相关试题
,焦点到渐近线的距离为
,求此双曲线的方程.
：对任意实数
都有
恒成立；
：关于
有实数根；如果
的取值范围．
所围成的正方形内掷一点，点落在该正方形内任何区域的概率与区域的面积成正比，求原点与该点的连线与x轴正方向夹角小于
的概率.
，乙能解决它的概率是
，现两人试图在30分钟内解决它，则推荐套卷
某中学校本课程共开设了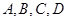共门选修课,每个学生必须且只能选修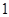门选修课,现有该校的甲、乙、丙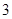名学生.
（Ⅰ）求这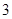名学生选修课所有选法的总数；
（Ⅱ）求恰有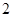门选修课没有被这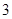名学生选择的概率；
（Ⅲ）求选修课被这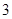名学生选择的人数的分布列和数学期望.
粤公网安备 44130202000953号