已知：△ABC是边长为4的等边三角形，点O在边AB上，⊙O过点B且分别与边AB，BC相交于点D，E，EF⊥AC，垂足为F.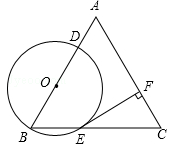
（1）求证：直线EF是⊙O的切线；
（2）当直线DF与⊙O相切时，求⊙O的半径.
相关试题
﹣
≥x﹣
，并把它的解集在数轴上表示出来．
相关知识点
推荐套卷
已知：△ABC是边长为4的等边三角形，点O在边AB上，⊙O过点B且分别与边AB，BC相交于点D，E，EF⊥AC，垂足为F.
（1）求证：直线EF是⊙O的切线；
（2）当直线DF与⊙O相切时，求⊙O的半径.
粤公网安备 44130202000953号