如图所示,在平面直角坐标系中,抛物线 (
( )经过A(-1,0)、B(3,0)两点,抛物线与y轴交点为C,其顶点为D,连接BD,点P是线段BD上一个动点(不与B,D重合),过点P作y轴的垂线,垂足为E,连接BE.
)经过A(-1,0)、B(3,0)两点,抛物线与y轴交点为C,其顶点为D,连接BD,点P是线段BD上一个动点(不与B,D重合),过点P作y轴的垂线,垂足为E,连接BE.
(1)求抛物线的解析式,并写出顶点D的坐标;
(2)如果P点的坐标为( ,
, ),△PBE的面积为
),△PBE的面积为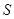 ,求
,求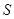 与
与 的函数关系式,写出自变量
的函数关系式,写出自变量 的取值范围.
的取值范围.
相关知识点
推荐套卷
如图所示,在平面直角坐标系中,抛物线 (
( )经过A(-1,0)、B(3,0)两点,抛物线与y轴交点为C,其顶点为D,连接BD,点P是线段BD上一个动点(不与B,D重合),过点P作y轴的垂线,垂足为E,连接BE.
)经过A(-1,0)、B(3,0)两点,抛物线与y轴交点为C,其顶点为D,连接BD,点P是线段BD上一个动点(不与B,D重合),过点P作y轴的垂线,垂足为E,连接BE.
(1)求抛物线的解析式,并写出顶点D的坐标;
(2)如果P点的坐标为( ,
, ),△PBE的面积为
),△PBE的面积为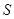 ,求
,求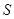 与
与 的函数关系式,写出自变量
的函数关系式,写出自变量 的取值范围.
的取值范围.