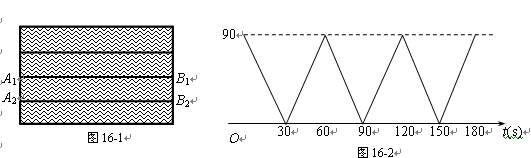
如图16-1,在一次航海模型船训练中,A1B1和A2B2是水面上相邻的两条赛道(看成两条互相平行的线段).甲船在赛道A1B1上从A1处出发,到达B1后,以同样的速度返回A1处,然后重复上述过程;乙船在赛道A2B2上以2m/s的速度从B2处出发,到达A2后以相同的速度回到B2处,然后重复上述过程(不考虑每次折返时的减速和转向时间).若甲、乙两船同时出发,设离开池边B1B2的距离为y(m),运动时间为t(s),甲船运动时,y(m)与t(s)的函数图象如图16-2所示.
![]()
赛道的长度是_________m,甲船的速度是________m/s;
![]()
分别求出甲船在0≤t≤30和30<t≤60时,y关于t的函数关系式;
![]()
求出乙船由B
2到达A
2的时间,并在图16-2中画出乙船在3 分钟内的函数图象
![]()
请你根据(3)中所画的图象直接判断,若从甲、乙两船同时开始出发到3分钟为止,甲、乙共相遇了几次?