某超市上月销售一种优质新米,平均售价为10元/千克,月销售量为1000千克。经市场调查,若将该种新米价格调低至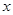 元/千克,则本月销售量
元/千克,则本月销售量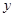 (千克)与
(千克)与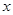 (元/千克)之间满足
(元/千克)之间满足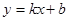 ,且当
,且当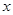 =7时,
=7时,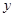 =2000;当
=2000;当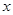 =5时,
=5时,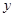 =4000.
=4000.
(1)求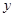 与
与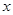 之间的函数关系式。
之间的函数关系式。
(2)已知该种新米上月的进价为5元/千克,本月的进价为4元/千克,要使本月销售该种新米获利比上月增加20%,同时又要让顾客得到实惠,则该种新米的价格应定为多少元?
相关知识点
推荐套卷
某超市上月销售一种优质新米,平均售价为10元/千克,月销售量为1000千克。经市场调查,若将该种新米价格调低至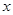 元/千克,则本月销售量
元/千克,则本月销售量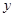 (千克)与
(千克)与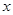 (元/千克)之间满足
(元/千克)之间满足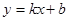 ,且当
,且当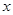 =7时,
=7时,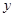 =2000;当
=2000;当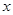 =5时,
=5时,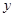 =4000.
=4000.
(1)求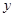 与
与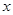 之间的函数关系式。
之间的函数关系式。
(2)已知该种新米上月的进价为5元/千克,本月的进价为4元/千克,要使本月销售该种新米获利比上月增加20%,同时又要让顾客得到实惠,则该种新米的价格应定为多少元?