如图,AB是☉O的直径,AM和BN是☉O的两条切线,E是☉O上一点,D是AM上一点,连接DE并延长交BN于点C,且OD∥BE,OF∥BN.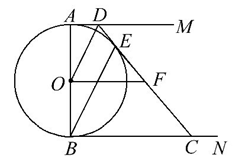 
（1）求证:DE是☉O的切线.
（2）求证:OF ＝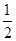
CD.
，4
相关知识点
推荐套卷
如图,AB是☉O的直径,AM和BN是☉O的两条切线,E是☉O上一点,D是AM上一点,连接DE并延长交BN于点C,且OD∥BE,OF∥BN.
（1）求证:DE是☉O的切线.
（2）求证:OF 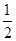＝CD.
粤公网安备 44130202000953号