（本小题满分13分）某风景区在一个直径AB为100米的半圆形花园中设计一条观光线路（如图所示）.在点A与圆弧上的一点C之间设计为直线段小路，在路的两侧边缘种植绿化带；从点C到点B设计为沿弧BC的弧形小路，在路的一侧边缘种植绿化带.（注：小路及绿化带的宽度忽略不计）
（1）设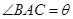
（弧度），将绿化带总长度表示为
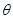的函数
；
（2）试确定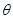的值，使得绿化带总长度最大.
相关试题
}，B={x|−1≤x<1},
；
，求
；
，且
，求
的取值范围．
与
，其中
是偶函数．
的值；
的定义域；
的取值范围．
中，
，求
的值．
在角
的终边上，点
在角β的终边上，点
在角
终边上．
，
，
的值；
的值．
；
．推荐套卷
（本小题满分13分）某风景区在一个直径AB为100米的半圆形花园中设计一条观光线路（如图所示）.在点A与圆弧上的一点C之间设计为直线段小路，在路的两侧边缘种植绿化带；从点C到点B设计为沿弧BC的弧形小路，在路的一侧边缘种植绿化带.（注：小路及绿化带的宽度忽略不计）
（1）设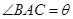（弧度），将绿化带总长度表示为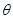的函数；
（2）试确定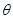的值，使得绿化带总长度最大.
粤公网安备 44130202000953号