市一中随机抽取部分高一学生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中上学路上所需时间的范围是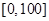 ,样本数据分组为
,样本数据分组为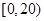 ,
,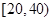 ,
,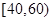 ,
,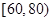 ,
,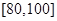 .
.
(Ⅰ)求直方图中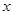 的值;
的值;
(Ⅱ)如果上学路上所需时间不少于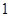 小时的学生可申请在学校住宿,若招生
小时的学生可申请在学校住宿,若招生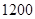 名,请估计新生中有多少名学生可以申请住宿;
名,请估计新生中有多少名学生可以申请住宿;
(Ⅲ)从学校的高一学生中任选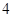 名学生,这
名学生,这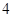 名学生中上学路上所需时间少于
名学生中上学路上所需时间少于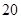 分钟的人数记为
分钟的人数记为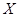 ,求
,求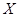 的分布列和数学期望.(以直方图中的频率作为概率)
的分布列和数学期望.(以直方图中的频率作为概率)
推荐套卷
市一中随机抽取部分高一学生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中上学路上所需时间的范围是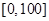 ,样本数据分组为
,样本数据分组为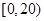 ,
,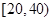 ,
,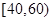 ,
,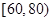 ,
,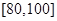 .
.
(Ⅰ)求直方图中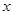 的值;
的值;
(Ⅱ)如果上学路上所需时间不少于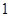 小时的学生可申请在学校住宿,若招生
小时的学生可申请在学校住宿,若招生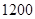 名,请估计新生中有多少名学生可以申请住宿;
名,请估计新生中有多少名学生可以申请住宿;
(Ⅲ)从学校的高一学生中任选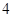 名学生,这
名学生,这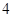 名学生中上学路上所需时间少于
名学生中上学路上所需时间少于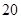 分钟的人数记为
分钟的人数记为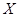 ,求
,求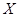 的分布列和数学期望.(以直方图中的频率作为概率)
的分布列和数学期望.(以直方图中的频率作为概率)