如图，在平面直角坐标系xOy中，一次函数y=kx+b的图象与x轴相交于点A（－３，０），与y轴交于点B，且与正比例函数y=
的图象交点为C（m，4）求：
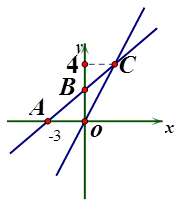
（1）一次函数y=kx+b的解析式；
（2）若点D在第二象限，△DAB是以AB为直角边的等腰直角三角形，直接写出点D的坐标。
（3）在x轴上求一点P使△POC为等腰三角形，请直接写出所有符合条件的点P的坐标．
，求(1)
；(2)
.
,求
的值.
.
；
大卡的能量，若每人每年要消耗
大卡的植物能量，试问地球能养活多少人？相关知识点
推荐套卷
如图，在平面直角坐标系xOy中，一次函数y=kx+b的图象与x轴相交于点A（－３，０），与y轴交于点B，且与正比例函数y=的图象交点为C（m，4）求：
（1）一次函数y=kx+b的解析式；
（2）若点D在第二象限，△DAB是以AB为直角边的等腰直角三角形，直接写出点D的坐标。
（3）在x轴上求一点P使△POC为等腰三角形，请直接写出所有符合条件的点P的坐标．
粤公网安备 44130202000953号