某宾馆有50个房间供游客住宿，当每个房间的房价为每天180元时，房间会全部住满．当每个房间 每天的房价每增加10元时，就会有一个房间空闲．宾馆需对游客居住的每个房间每天支出20元的各种费用．根据规定，每个房间每天的房价不得高于340元．设每个房间的房价增加x元（x为10的正整数倍）．
（1）设一天订住的房间数为y，直接写出y与x的函数关系式及自变量x的取值范围；
（2）设宾馆一天的利润为w元，求w与x的函数关系式；
（3）一天订住多少个房间时，宾馆的利润最大？最大利润是多少元？
，求这个正方体的表面积（结果保留4个有效数字）
，你能从中找出计算规律吗？如果将根号内的数10换成
，这种计算规律是否仍然存在，你能用公式表示上述计算规律吗？
和
的大小.
；（2）
；（3）
；（4）
，求正方体的棱长（保留3个有效数字）相关知识点
推荐套卷
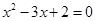粤公网安备 44130202000953号