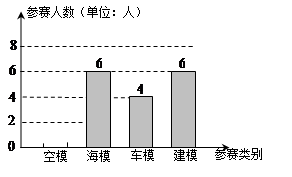
为进一步促进青少年科技模型教育的普及和发展,丰富校园科技体育活动,某市6月份将举行中小学科技运动会。下图为某校将参加科技运动会航模比赛(包括空模、海模、车模、建模四个类别)的参赛人数统计图:
(1)该校参加航模比赛的总人数是 人,空模所在扇形的圆心角的度数是 ;
(2)把条形统计图补充完整;
(3)从全市中小学参加航模比赛选手中随机抽取80人,其中有32人获奖.今年该市中小学参加航模比赛人数共2485人,请你估算今年参加航模比赛的获奖人数约是多少人?
|
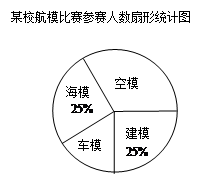
相关知识点
推荐套卷

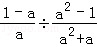 .
.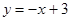 交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.
交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.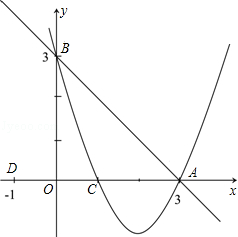
 粤公网安备 44130202000953号
粤公网安备 44130202000953号