模型建立:如图,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于D,过B作BE⊥ED于E。
求证:△BEC≌△CDA
模型应用:
(1)已知直线 与y轴交与A点,将直线
与y轴交与A点,将直线 绕着A点顺时针旋转
绕着A点顺时针旋转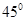 至
至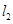 ,求
,求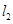 的函数解析式。
的函数解析式。
(2)如图,矩形ABCO,O为坐标原点,B的坐标为(8,6),A、C分别在坐标轴上,P是线段BC上动点,设PC=m,已知点D在第一象限,且是直线y=2x-6上的一点,若△APD是不以A为直角顶点的等腰Rt△,请直接写出点D的坐标。
推荐套卷
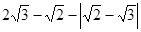 (2)
(2)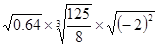
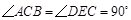 ,
,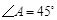 ,
,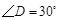 ,斜边
,斜边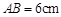 ,
, .把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙).这时AB与CD1相交于点
.把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙).这时AB与CD1相交于点 、与D1E1相交于点F.
、与D1E1相交于点F.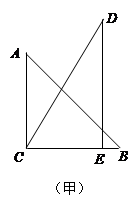
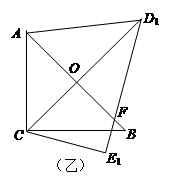
 的度数;
的度数;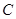 顺时针再旋转30°得△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?请说明理由。
顺时针再旋转30°得△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?请说明理由。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号