(本小题满分12分)广东某高中进行高中生歌唱比赛,在所有参赛成绩中随机抽取 名学生的成绩,按成绩分组:第
名学生的成绩,按成绩分组:第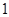 组
组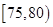 ,第
,第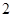 组
组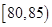 ,第
,第 组
组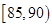 ,第
,第 组
组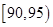 ,第
,第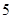 组
组 得到的频率分布直方图如图所示.现在组委会决定在笔试成绩高的第
得到的频率分布直方图如图所示.现在组委会决定在笔试成绩高的第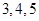 组中用分层抽样抽取
组中用分层抽样抽取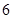 名学生进入第二轮面试.
名学生进入第二轮面试.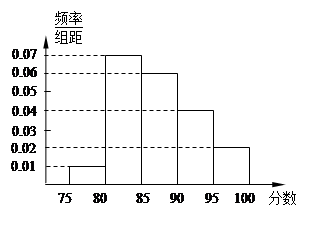
(1)求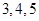 组各应抽取多少人进入第二轮面试;
组各应抽取多少人进入第二轮面试;
(2)学校决定在(1)中抽取的这6名学生中随机抽取2名学生接受考官D的面试,求第四组中至少一人被考官D面试的概率.
推荐套卷
(本小题满分12分)广东某高中进行高中生歌唱比赛,在所有参赛成绩中随机抽取 名学生的成绩,按成绩分组:第
名学生的成绩,按成绩分组:第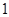 组
组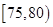 ,第
,第 组
组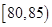 ,第
,第 组
组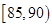 ,第
,第 组
组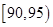 ,第
,第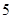 组
组 得到的频率分布直方图如图所示.现在组委会决定在笔试成绩高的第
得到的频率分布直方图如图所示.现在组委会决定在笔试成绩高的第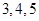 组中用分层抽样抽取
组中用分层抽样抽取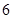 名学生进入第二轮面试.
名学生进入第二轮面试.
(1)求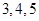 组各应抽取多少人进入第二轮面试;
组各应抽取多少人进入第二轮面试;
(2)学校决定在(1)中抽取的这6名学生中随机抽取2名学生接受考官D的面试,求第四组中至少一人被考官D面试的概率.