（本小题满分12分）
已知椭圆
的离心率为e=
，且过点（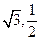
）
（Ⅰ）求椭圆的方程；
（Ⅱ）设直线l：y=kx+m(k≠0，m＞0)与椭圆交于P，Q两点，且以PQ为对角线的菱形的一顶点为（-1，0），求：△OPQ面积的最大值及此时直线l的方程.
能被9整除．
条直线，其中任何两条不平行，任何三条不过同一点，证明这
个部分
，若
，并猜想
满足条件：
，
（
），且
是公比为q （
）的等比数列．设
（
），求
与
，其中
相关知识点
推荐套卷
（本小题满分12分）
已知椭圆的离心率为e=，且过点（）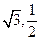
（Ⅰ）求椭圆的方程；
（Ⅱ）设直线l：y=kx+m(k≠0，m＞0)与椭圆交于P，Q两点，且以PQ为对角线的菱形的一顶点为（-1，0），求：△OPQ面积的最大值及此时直线l的方程.
粤公网安备 44130202000953号