（本小题满分12分）
如图，平面ABCD⊥平面PAD，△APD是直角三角形，
∠APD=90°，四边形ABCD是直角梯形，其中BC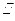
AD，
∠BAD=90°，AD="2" BC，且AB=BC=PD=2，O是AD的中点，E，F分别是PC，OD的中点.
（Ⅰ）求证：EF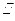平面PBO；
（Ⅱ）求二面角A- PF - E的正切值.
相关试题
,其中
,命题
实数
满足
.
且
为真，求实数
是
的充分不必要条件,求实数
的取值范围.
是一个公差为
的等差数列，它的前
，且
成等比数列。
前n项之和。
前n项之和
的直线，被抛物线所截得的弦长为8，试求抛物线的标准方程.
，其中a<0;q:实数x满足
且
的必要不充分条件，求a的范围.推荐套卷
（本小题满分12分）
如图，平面ABCD⊥平面PAD，△APD是直角三角形，
∠APD=90°，四边形ABCD是直角梯形，其中BC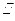AD，
∠BAD=90°，AD="2" BC，且AB=BC=PD=2，O是AD的中点，E，F分别是PC，OD的中点.
（Ⅰ）求证：EF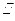平面PBO；
（Ⅱ）求二面角A- PF - E的正切值.
粤公网安备 44130202000953号