(本小题满分12分)如图,圆 的方程为
的方程为 ,
, 是圆
是圆 外一个定点,
外一个定点, 是线段
是线段 的中点,
的中点,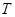 是圆上任意一点,线段
是圆上任意一点,线段 的垂直平分线
的垂直平分线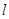 和半径
和半径 所在直线相交于点
所在直线相交于点 .
.
(Ⅰ)当点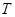 在圆上运动时,求证:点
在圆上运动时,求证:点 的轨迹
的轨迹 为双曲线,并求轨迹
为双曲线,并求轨迹 的方程;
的方程;
(Ⅱ)若 是双曲线
是双曲线 的左顶点,设过双曲线
的左顶点,设过双曲线 右焦点
右焦点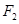 的直线
的直线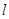 与双曲线
与双曲线 的右支交于
的右支交于 两点,其中点位于第一象限内.若直线
两点,其中点位于第一象限内.若直线 分别与直线
分别与直线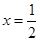 交于
交于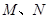 两点,求证:
两点,求证: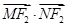 为定值;
为定值;
相关知识点
推荐套卷
(本小题满分12分)如图,圆 的方程为
的方程为 ,
, 是圆
是圆 外一个定点,
外一个定点, 是线段
是线段 的中点,
的中点,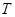 是圆上任意一点,线段
是圆上任意一点,线段 的垂直平分线
的垂直平分线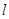 和半径
和半径 所在直线相交于点
所在直线相交于点 .
.
(Ⅰ)当点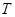 在圆上运动时,求证:点
在圆上运动时,求证:点 的轨迹
的轨迹 为双曲线,并求轨迹
为双曲线,并求轨迹 的方程;
的方程;
(Ⅱ)若 是双曲线
是双曲线 的左顶点,设过双曲线
的左顶点,设过双曲线 右焦点
右焦点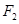 的直线
的直线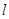 与双曲线
与双曲线 的右支交于
的右支交于 两点,其中点位于第一象限内.若直线
两点,其中点位于第一象限内.若直线 分别与直线
分别与直线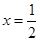 交于
交于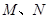 两点,求证:
两点,求证: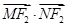 为定值;
为定值;