某单位有员工1000名,平均每人每年创造利润10万元.为了增加企业竞争力,决定优化产业结构,调整出x (x∈ )名员工从事第三产业,调整后他们平均每人每年创造利润为
)名员工从事第三产业,调整后他们平均每人每年创造利润为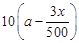 万元(a>0),剩下的员工平均每人每年创造的利润可以提高0.2x%.
万元(a>0),剩下的员工平均每人每年创造的利润可以提高0.2x%.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?
(2)在(1)的条件下,若调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,则a的取值范围是多少?
推荐套卷
某单位有员工1000名,平均每人每年创造利润10万元.为了增加企业竞争力,决定优化产业结构,调整出x (x∈ )名员工从事第三产业,调整后他们平均每人每年创造利润为
)名员工从事第三产业,调整后他们平均每人每年创造利润为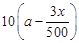 万元(a>0),剩下的员工平均每人每年创造的利润可以提高0.2x%.
万元(a>0),剩下的员工平均每人每年创造的利润可以提高0.2x%.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?
(2)在(1)的条件下,若调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,则a的取值范围是多少?