如图所示,正方形 所在的平面与等腰
所在的平面与等腰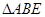 所在的平面互相垂直,其中顶
所在的平面互相垂直,其中顶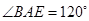 ,
, ,
,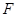 为线段
为线段 的中点.
的中点.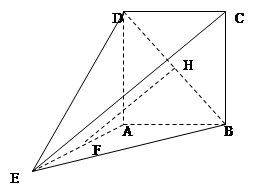
(Ⅰ)若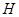 是线段
是线段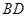 上的中点,求证:
上的中点,求证: // 平面
// 平面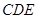 ;
;
(Ⅱ)若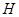 是线段
是线段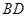 上的一个动点,设直线
上的一个动点,设直线 与平面
与平面 所成角的大小为
所成角的大小为 ,求
,求 的最大值.
的最大值.
推荐套卷
如图所示,正方形 所在的平面与等腰
所在的平面与等腰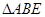 所在的平面互相垂直,其中顶
所在的平面互相垂直,其中顶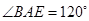 ,
, ,
,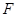 为线段
为线段 的中点.
的中点.
(Ⅰ)若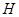 是线段
是线段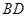 上的中点,求证:
上的中点,求证: // 平面
// 平面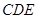 ;
;
(Ⅱ)若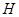 是线段
是线段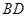 上的一个动点,设直线
上的一个动点,设直线 与平面
与平面 所成角的大小为
所成角的大小为 ,求
,求 的最大值.
的最大值.