（本小题14分）已知函数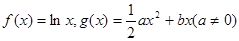
（Ⅰ）若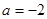
时，函数
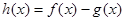在其定义域上是增函数，求b的取值范围；
（Ⅱ）在（Ⅰ）的结论下，设函数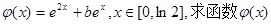
的最小值；
（Ⅲ）设函数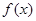
的图象C1与函数
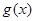的图象C2交于P、Q，过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N，问是否存在点R，使C1在M处的切线与C2在N处的切线平行？若存在，求出R的横坐标；若不存在，请说明理由.
,
,
,求
取值范围; 
的最值，并给出最值时对应的x的值。
且
的取值范围。
,A、B是U的子集,同时满足
求A和B .
,
且
求
的值.推荐套卷
（本小题14分）已知函数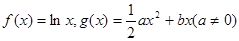
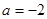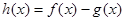（Ⅰ）若时，函数在其定义域上是增函数，求b的取值范围；
（Ⅱ）在（Ⅰ）的结论下，设函数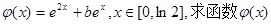的最小值；
（Ⅲ）设函数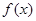的图象C1与函数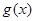的图象C2交于P、Q，过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N，问是否存在点R，使C1在M处的切线与C2在N处的切线平行？若存在，求出R的横坐标；若不存在，请说明理由.
粤公网安备 44130202000953号