（本小题满分12分）已知函数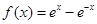
，其中e是自然对数的底数.
（Ⅰ）证明：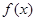
是R上的奇函数；
（Ⅱ）若关于x的不等式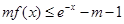
在
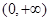上恒成立，求实数m的取值范围；
（Ⅲ）已知正数a满足：存在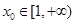
，使得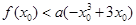
成立，试比较
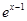与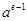
的大小，并证明你的结论.
相关试题
推荐套卷
（本小题满分12分）已知函数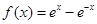，其中e是自然对数的底数.
（Ⅰ）证明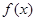：是R上的奇函数；
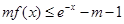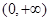（Ⅱ）若关于x的不等式在上恒成立，求实数m的取值范围；
（Ⅲ）已知正数a满足：存在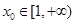，使得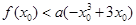成立，试比较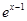与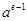的大小，并证明你的结论.
粤公网安备 44130202000953号