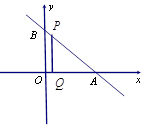
（本小题10分）如图直线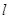
过点（3,4）, 与
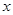轴、
轴的正半轴分别交于A、B两点，△ABC的面积为24. 点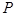
为线段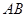
上一动点，且
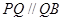交
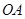于点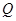
．
（Ⅰ）求直线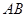斜率的大小；
（Ⅱ）若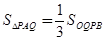
时，请你确定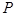点在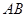上的位置，并求出线段
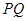的长；
（Ⅲ）在轴上是否存在点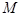
，使△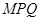
为等腰直角三角形，若存在，求出点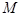的坐标；若不存在，说明理由.
相关试题
，
．
是函数
图象的一条对称轴，求
的值；
的单调递增区间．
．
的最小正周期；
上的最大值和最小值，并求函数取得最大值和最小值时的自变量
的值．
．
、
为锐角，且
，
，求
的值． 
.
.
.
，当 B1D⊥面PMN时，求
的值.
推荐套卷
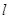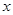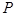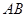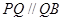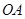（本小题10分）如图直线过点（3,4）, 与轴、轴的正半轴分别交于A、B两点，△ABC的面积为24. 点为线段上一动点，且交于点．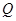
（Ⅰ）求直线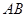斜率的大小；
（Ⅱ）若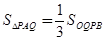时，请你确定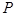点在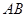上的位置，并求出线段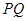的长；
（Ⅲ）在轴上是否存在点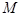，使△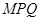为等腰直角三角形，若存在，求出点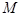的坐标；若不存在，说明理由.
粤公网安备 44130202000953号