(原创)(本小题满分12分)已知点 点P在
点P在 轴上,点Q在
轴上,点Q在 轴正半轴上,点M在
轴正半轴上,点M在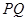 上,且满足
上,且满足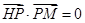 ,
, .
.
(1)当点P在 轴上移动时,求点M的轨迹方程C;
轴上移动时,求点M的轨迹方程C;
(2)给定圆N: 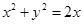 ,过圆心N作直线
,过圆心N作直线 ,此直线与圆N和(1)中的轨迹C共有四个交点,自上而下顺次记为A,B,C,D,如果线段
,此直线与圆N和(1)中的轨迹C共有四个交点,自上而下顺次记为A,B,C,D,如果线段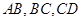 的长按此顺序构成一个等差数列,求直线
的长按此顺序构成一个等差数列,求直线 的方程。
的方程。
相关知识点
推荐套卷
(原创)(本小题满分12分)已知点 点P在
点P在 轴上,点Q在
轴上,点Q在 轴正半轴上,点M在
轴正半轴上,点M在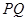 上,且满足
上,且满足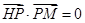 ,
, .
.
(1)当点P在 轴上移动时,求点M的轨迹方程C;
轴上移动时,求点M的轨迹方程C;
(2)给定圆N: 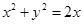 ,过圆心N作直线
,过圆心N作直线 ,此直线与圆N和(1)中的轨迹C共有四个交点,自上而下顺次记为A,B,C,D,如果线段
,此直线与圆N和(1)中的轨迹C共有四个交点,自上而下顺次记为A,B,C,D,如果线段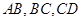 的长按此顺序构成一个等差数列,求直线
的长按此顺序构成一个等差数列,求直线 的方程。
的方程。