（能力提升）定义在R上的单调函数f（x）满足f（3）=log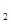
3且对任意x，y∈R都有f（x+y）=f（x）+f（y）．
（1）求证f（x）为奇函数；
（2）若f（k·3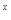
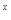）+f（3-9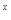-2）＜0对任意x∈R恒成立，求实数k的取值范围．
相关试题
BD.
ABC
.
的单调区间；
对定义域每的任意
恒成立，求实数
的取值范围；
，不等式
恒成立。
的底面
位于平行四边形
中,
,
,
,点
为
中点.
平面
.
的大小为
,直线
与平面
所成的角为
,求
的值.
推荐套卷
（能力提升）定义在R上的单调函数f（x）满足f（3）=log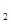3且对任意x，y∈R都有f（x+y）=f（x）+f（y）．
（1）求证f（x）为奇函数；
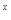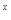（2）若f（k·3）+f（3-9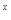-2）＜0对任意x∈R恒成立，求实数k的取值范围．
粤公网安备 44130202000953号