如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
（1）求证:AA1⊥平面ABC;
（2）求二面角A1-BC1-B1的余弦值;
（3）证明:在线段BC1存在点D,使得AD⊥A1B,并求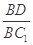
的值.
相关试题
中，三边a,b,c满足：
.
的最高次项系数为a，三个零点分别为
. 
有两个相等的实根，求a的值；
在区间
内单调递减，求a的取值范围.
中，
，
平面
；
∥平面
中，点
在角
的终边上，点
在角
的终边上，且
的值；⑵求
的值。
与曲线
只有一个公共点，求实数
的取值范围；
与曲线
和
，且
（其中
为坐标原点），求实数
的取值范围。推荐套卷
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
（1）求证:AA1⊥平面ABC;
（2）求二面角A1-BC1-B1的余弦值;
（3）证明:在线段BC1存在点D,使得AD⊥A1B,并求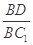的值.
粤公网安备 44130202000953号