(本小题满分12分)在国家法定工作日内，每周满工作量的时间为40小时，若每周工作时间不超过40小时，则每小时工资25元；如因需要加班，超过40小时的每小时工资为50元．某公务员在一周内工作时间为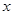
小时，但他须交纳个人住房公积金和失业保险(这两项费用为每周总收入的10%)．试分析算法步骤并画出其每周净得工资
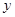元的算法的程序框图．(注：满工作量外的工作时间为加班)
相关试题
。
成立的
的取值范围；
的最小值。
定义在R上的偶函数，当
时，
.
的定义域；（2）判断
的图象经过点
，其中
且
。
的值；
； 
推荐套卷
(本小题满分12分)在国家法定工作日内，每周满工作量的时间为40小时，若每周工作时间不超过40小时，则每小时工资25元；如因需要加班，超过40小时的每小时工资为50元．某公务员在一周内工作时间为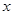小时，但他须交纳个人住房公积金和失业保险(这两项费用为每周总收入的10%)．试分析算法步骤并画出其每周净得工资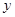元的算法的程序框图．(注：满工作量外的工作时间为加班)
粤公网安备 44130202000953号