(本题13分)已知某种植物种子每粒成功发芽的概率都为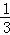 ,某植物研究所进行该种子的发芽实验,每次实验种一粒种子,每次实验结果相互独立.假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.若该研究所共进行四次实验,设ξ表示四次实验结束时实验成功的次数与失败的次数之差的绝对值;
,某植物研究所进行该种子的发芽实验,每次实验种一粒种子,每次实验结果相互独立.假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.若该研究所共进行四次实验,设ξ表示四次实验结束时实验成功的次数与失败的次数之差的绝对值;
(1)求随机变量ξ的数学期望;
(2)记“关于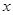 的不等式
的不等式 的解集是实数集R”为事件A,求事件A发生的概率
的解集是实数集R”为事件A,求事件A发生的概率 .
.
推荐套卷
(本题13分)已知某种植物种子每粒成功发芽的概率都为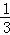 ,某植物研究所进行该种子的发芽实验,每次实验种一粒种子,每次实验结果相互独立.假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.若该研究所共进行四次实验,设ξ表示四次实验结束时实验成功的次数与失败的次数之差的绝对值;
,某植物研究所进行该种子的发芽实验,每次实验种一粒种子,每次实验结果相互独立.假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.若该研究所共进行四次实验,设ξ表示四次实验结束时实验成功的次数与失败的次数之差的绝对值;
(1)求随机变量ξ的数学期望;
(2)记“关于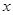 的不等式
的不等式 的解集是实数集R”为事件A,求事件A发生的概率
的解集是实数集R”为事件A,求事件A发生的概率 .
.