(南京市2002年二模)某公司生产的A型商品通过租赁柜台进入某商场销售.第一年,商 场为吸引厂家,决定免收该年管理费,因此,该年A型商品定价为每件70元,销售量为 11.8万件.第二年,商场开始对该商品征收比率为p%的管理费(即每销售100元要征收p元),于是该商品的定价上升为每件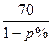 元,预计年销售量将减少p万件.
元,预计年销售量将减少p万件.
(1)将第二年商场对商品征收的管理费y(万元)表示成p的函数,并指出这个函数的定义域;
(2)要使第二年商场在此项经营中收取的管理费不少于14万元,则商场对该商品征收管理费的比率p%的范围是多少?
(3)第二年,商场在所收费不少于14万元的前提下,要让厂家获得最大销售金额,则p 应为多少?