如图,海上有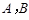 两个小岛相距10
两个小岛相距10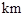 ,船O将保持观望A岛和B岛所成的视角为
,船O将保持观望A岛和B岛所成的视角为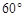 ,现从船O上派下一只小艇沿
,现从船O上派下一只小艇沿 方向驶至
方向驶至 处进行作业,且
处进行作业,且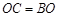 .设
.设
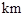 。
。
(1)用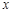 分别表示
分别表示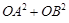 和
和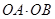 ,并求出
,并求出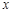 的取值范围;
的取值范围;
(2)晚上小艇在 处发出一道强烈的光线照射A岛,B岛至光线
处发出一道强烈的光线照射A岛,B岛至光线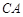 的距离为
的距离为 ,求BD的最大值.
,求BD的最大值.
推荐套卷
如图,海上有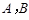 两个小岛相距10
两个小岛相距10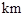 ,船O将保持观望A岛和B岛所成的视角为
,船O将保持观望A岛和B岛所成的视角为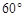 ,现从船O上派下一只小艇沿
,现从船O上派下一只小艇沿 方向驶至
方向驶至 处进行作业,且
处进行作业,且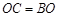 .设
.设
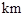 。
。
(1)用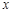 分别表示
分别表示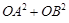 和
和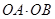 ,并求出
,并求出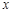 的取值范围;
的取值范围;
(2)晚上小艇在 处发出一道强烈的光线照射A岛,B岛至光线
处发出一道强烈的光线照射A岛,B岛至光线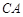 的距离为
的距离为 ,求BD的最大值.
,求BD的最大值.