（本小题满分12分）已知椭圆E的方程：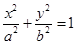
（
），它的两个焦点为
，P为椭圆的一点（点
在第三象限上）, 且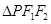
的周长为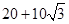
，
（Ⅰ）求椭圆E的方程；
（Ⅱ）若以点P为圆心的圆过椭圆的左顶点M与点
， MP交圆P与另一点N,若点A在椭圆E上，使得
，求点A的坐标.
相关试题
为等比数列，
为其前
项和，已知
.
的通项公式；
的前
项和
．
的焦点为焦点，且过
点的双曲线的标准方程.
上的点
到左右两焦点
的距离之和为
，离心率为
.
的直线
交椭圆于
两点，若
轴上一点
满足
，求直线
的值.
，其准线方程为
，过准线与
轴的交点
做直线
交抛物线于
两点.
为
中点，求直线
，当
时，求
的面积．
，
面
,
∥
,
,
，
,
,
为
上一点,
是平面
与
的交点.
∥
面
；
与面推荐套卷
（本小题满分12分）已知椭圆E的方程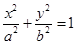：（），它的两个焦点为，P为椭圆的一点（点在第三象限上）, 且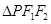的周长为，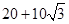
（Ⅰ）求椭圆E的方程；
（Ⅱ）若以点P为圆心的圆过椭圆的左顶点M与点， MP交圆P与另一点N,若点A在椭圆E上，使得 ，求点A的坐标.
粤公网安备 44130202000953号