已知：在△ABC中，AC=BC，∠ACB=90°，点D是AB的中点，点E是AB边上一点．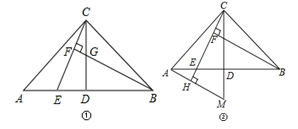
（1）直线BF垂直于直线CE于点F，交CD于点G（如图①），求证：AE=CG；
（2）直线AH垂直于直线CE，垂足为点 H，交CD的延长线于点M（如图②），找出图中与BE相等的线段，并证明．
相关试题
(1)作∠AOB角平分线(2)作线段AB垂直平分线
△DEF
相关知识点
推荐套卷
已知：在△ABC中，AC=BC，∠ACB=90°，点D是AB的中点，点E是AB边上一点．
（1）直线BF垂直于直线CE于点F，交CD于点G（如图①），求证：AE=CG；
（2）直线AH垂直于直线CE，垂足为点 H，交CD的延长线于点M（如图②），找出图中与BE相等的线段，并证明．
粤公网安备 44130202000953号