某幢大楼顶部有一块广告牌CD,甲、乙两人分别在相距8米的A,B两处测得D点和C点的仰角分别为45°和60°,且A,B,E三点在一条直线上,若
BE=15米,求这块广告牌的高度.(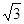 ≈1.73,结果保留整数)
≈1.73,结果保留整数)
相关知识点
推荐套卷
某幢大楼顶部有一块广告牌CD,甲、乙两人分别在相距8米的A,B两处测得D点和C点的仰角分别为45°和60°,且A,B,E三点在一条直线上,若
BE=15米,求这块广告牌的高度.(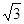 ≈1.73,结果保留整数)
≈1.73,结果保留整数)