如图,已知点A (0,4) 和点B (3,0)都在抛物线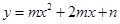 上.
上.
(1)求 、n;
、n;
(2)向右平移上述抛物线,记平移后点A的对应点为D,点B的对应点为C,若四边形A BCD为菱形,求平移后抛物线的表达式;
(3)记平移后抛物线的对称轴与直线AC的交点为点E,试在 轴上找点F,使得以点C、E、F为顶点的三角形与△ ABE相似。
轴上找点F,使得以点C、E、F为顶点的三角形与△ ABE相似。
相关知识点
推荐套卷
如图,已知点A (0,4) 和点B (3,0)都在抛物线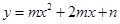 上.
上.
(1)求 、n;
、n;
(2)向右平移上述抛物线,记平移后点A的对应点为D,点B的对应点为C,若四边形A BCD为菱形,求平移后抛物线的表达式;
(3)记平移后抛物线的对称轴与直线AC的交点为点E,试在 轴上找点F,使得以点C、E、F为顶点的三角形与△ ABE相似。
轴上找点F,使得以点C、E、F为顶点的三角形与△ ABE相似。