平面直角坐标系中,M(36,0),⊿OMN是等腰直角三角形,∠ONM=90°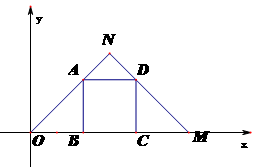
(1) 直接写出N的坐标;
(2) 正方形ABCD是⊿OMN的内接正方形,求正方形边长;
(3) 在(2)的情况下,点P为线段AB上一点,以P为圆心,PB为半径的圆交线段AD于点E.当B,E,N在一条直线上时,求⊙P半径;
(4) 在(3)的情况下,线段CD上取点F,使∠EBF=45°,连结EF,判断直线EF与⊙P是否相切.若是,写出推理过程;若不是,说明理由.
相关知识点
推荐套卷
 ,4).
,4).
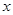 在什么范围内时,一次函数的值大于反比例函数的值?
在什么范围内时,一次函数的值大于反比例函数的值?
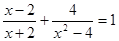
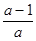 ÷
÷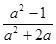 ,其中
,其中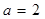
 粤公网安备 44130202000953号
粤公网安备 44130202000953号