 为一个等腰三角形形状的空地,腰
为一个等腰三角形形状的空地,腰 的长为3(百米),底
的长为3(百米),底 的长为4(百米).现决定在空地内筑一条笔直的小路
的长为4(百米).现决定在空地内筑一条笔直的小路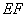 (宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等,面积分别为
(宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等,面积分别为 和
和 .
.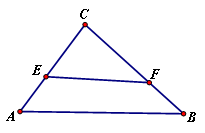
(1)若小路一端 为
为 的中点,求此时小路的长度;
的中点,求此时小路的长度;
(2)若小路的端点 两点分别在两腰上,求
两点分别在两腰上,求 得最小值.
得最小值.
推荐套卷
 为一个等腰三角形形状的空地,腰
为一个等腰三角形形状的空地,腰 的长为3(百米),底
的长为3(百米),底 的长为4(百米).现决定在空地内筑一条笔直的小路
的长为4(百米).现决定在空地内筑一条笔直的小路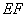 (宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等,面积分别为
(宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等,面积分别为 和
和 .
.
(1)若小路一端 为
为 的中点,求此时小路的长度;
的中点,求此时小路的长度;
(2)若小路的端点 两点分别在两腰上,求
两点分别在两腰上,求 得最小值.
得最小值.