(本小题满分14分)已知函数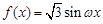
 的部分图像如图所示.
的部分图像如图所示.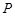 、
、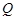 分别是图像上的一个最高点和最低点,
分别是图像上的一个最高点和最低点, 为图像与
为图像与 轴的交点,且四边形
轴的交点,且四边形 为矩形.
为矩形.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)将 的图像向右平移
的图像向右平移 个单位长度后,得到函数
个单位长度后,得到函数 的图像.已知
的图像.已知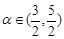 ,
, ,求
,求 的值.
的值.
相关知识点
推荐套卷
(本小题满分14分)已知函数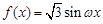
 的部分图像如图所示.
的部分图像如图所示.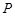 、
、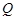 分别是图像上的一个最高点和最低点,
分别是图像上的一个最高点和最低点, 为图像与
为图像与 轴的交点,且四边形
轴的交点,且四边形 为矩形.
为矩形.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)将 的图像向右平移
的图像向右平移 个单位长度后,得到函数
个单位长度后,得到函数 的图像.已知
的图像.已知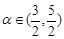 ,
, ,求
,求 的值.
的值.