(本小题满分12分)如图所示,某小区为美化环境,准备在小区内草坪的一侧修建一条直路OC;另一侧修建一条休闲大道,它的前一段OD是函数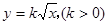 的一部分,后一段DBC是函数
的一部分,后一段DBC是函数 时的图象,图象的最高点为
时的图象,图象的最高点为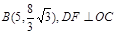 ,垂足为F.
,垂足为F.
(1)求函数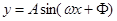 的解析式;
的解析式;
(2)若在草坪内修建如图所示的儿童游乐园PMFE,问点P落在曲线OD上何处时,儿童乐园的面积最大?
推荐套卷
(本小题满分12分)如图所示,某小区为美化环境,准备在小区内草坪的一侧修建一条直路OC;另一侧修建一条休闲大道,它的前一段OD是函数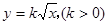 的一部分,后一段DBC是函数
的一部分,后一段DBC是函数 时的图象,图象的最高点为
时的图象,图象的最高点为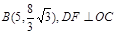 ,垂足为F.
,垂足为F.
(1)求函数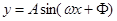 的解析式;
的解析式;
(2)若在草坪内修建如图所示的儿童游乐园PMFE,问点P落在曲线OD上何处时,儿童乐园的面积最大?