(本小题满分12分)
已知函数f(x)=ax3+bx2+cx+d在(-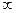 ,1)上单调递减,在(1,3)上单调递增,在(3,+
,1)上单调递减,在(1,3)上单调递增,在(3,+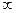 )上单调递减、且函数图象在(2,f(2))处的切线与直线5x+y=0垂直。
)上单调递减、且函数图象在(2,f(2))处的切线与直线5x+y=0垂直。
(Ⅰ)求实数a、b、c的值;
(Ⅱ)设方程f(x)=0有三个不相等的实数根,求d的取值范围 。
。
推荐套卷
(本小题满分12分)
已知函数f(x)=ax3+bx2+cx+d在(-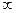 ,1)上单调递减,在(1,3)上单调递增,在(3,+
,1)上单调递减,在(1,3)上单调递增,在(3,+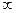 )上单调递减、且函数图象在(2,f(2))处的切线与直线5x+y=0垂直。
)上单调递减、且函数图象在(2,f(2))处的切线与直线5x+y=0垂直。
(Ⅰ)求实数a、b、c的值;
(Ⅱ)设方程f(x)=0有三个不相等的实数根,求d的取值范围 。
。