已知函数
的值满足
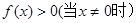，对任意实数x、y都有
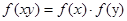，且f（－1）＝1，f（27）＝9，当0<x<1时，
.
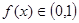（1）求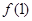
的值，判断的奇偶性并证明；
（2）判断在（0，＋∞）上的单调性，并给出证明；
（3）若
且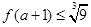
，求a的取值范围。
的定义域与值域
，
，求下列各式的值：
对一切
恒成立的负数
的取值范围是___________.
轴所得弦长为2；②被
轴分成两段圆弧，其弧长的比为
；③圆心到直线
的距离为
，求该圆的方程.相关知识点
推荐套卷
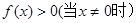已知函数的值满足，对任意实数x、y都有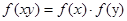，且f（－1）＝1，f（27）＝9，当0<x<1时，.
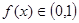（1）求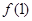的值，判断的奇偶性并证明；
（2）判断在（0，＋∞）上的单调性，并给出证明；
（3）若且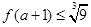，求a的取值范围。
粤公网安备 44130202000953号