(本小题满分14分)已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2的菱形, AC∩BD="O," AA1=2 , BD⊥A1A, ∠BAD=∠A1AC="60°," 点M是棱AA1的中点.
, BD⊥A1A, ∠BAD=∠A1AC="60°," 点M是棱AA1的中点.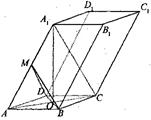
(1)求证: A1C∥平面BMD;
(2)求证: A1O⊥平面ABCD;
(3)求直线BM与平面BC1D所成角的正弦值.
推荐套卷
(本小题满分14分)已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2的菱形, AC∩BD="O," AA1=2 , BD⊥A1A, ∠BAD=∠A1AC="60°," 点M是棱AA1的中点.
, BD⊥A1A, ∠BAD=∠A1AC="60°," 点M是棱AA1的中点.
(1)求证: A1C∥平面BMD;
(2)求证: A1O⊥平面ABCD;
(3)求直线BM与平面BC1D所成角的正弦值.