为了探索函数
的图象与性质,我们参照学习函数的过程与方法.
列表:
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
描点:在平面直角坐标系中,以自变量
的取值为横坐标,以相应的函数值
为纵坐标,描出相应的点,如图1所示:
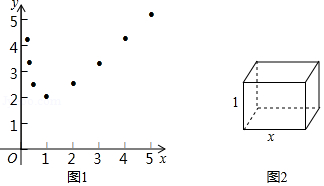
(1)如图1,观察所描出点的分布,用一条光滑曲线将点顺次连接起来,作出函数图象;
(2)已知点
,
,
,
在函数图象上,结合表格和函数图象,回答下列问题:
若
,则
;若
,则
;
若
,则
(填"
","
"或"
"
.
(3)某农户要建造一个图2所示的长方体形无盖水池,其底面积为1平方米,深为1米.已知底面造价为1千元
平方米,侧面造价为0.5千元
平方米.设水池底面一边的长为
米,水池总造价为
千元.
①请写出
与
的函数关系式;
②若该农户预算不超过3.5千元,则水池底面一边的长
应控制在什么范围内?

 粤公网安备 44130202000953号
粤公网安备 44130202000953号