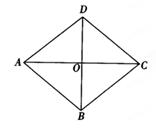
如图,菱形ABCD中,AC,BD交于O,AC=8m,BD=6m,动点M从A出发沿AC方向以2m/s匀速直线运动到C,动点N从B出发沿BD方向以1m/s匀速直线运动到D,若M,N同时出发,问出发后几秒钟时,△MON的面积为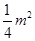 ?
?
推荐套卷
如图,菱形ABCD中,AC,BD交于O,AC=8m,BD=6m,动点M从A出发沿AC方向以2m/s匀速直线运动到C,动点N从B出发沿BD方向以1m/s匀速直线运动到D,若M,N同时出发,问出发后几秒钟时,△MON的面积为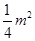 ?
?