（满分13分）如图所示，正四棱锥P－ABCD中，O为底面正方形的中心，侧棱PA与底面ABCD所成的角的正切值为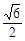
．
（1）求侧面PAD与底面ABCD所成的二面角的大小；
（2）若E是PB的中点，求异面直线PD与AE所成角的正切值；
（3）问在棱AD上是否存在一点F，使EF⊥侧面PBC，若存在，试确定点F的位置；若不存在，说明理由．
的奇偶性；
,
,求
；
的值。
是两个不共线的向量，，若A、B、D三点共线，求k的值.
中的x的取值范围.
相关知识点
推荐套卷
（满分13分）如图所示，正四棱锥P－ABCD中，O为底面正方形的中心，侧棱PA与底面ABCD所成的角的正切值为．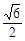
（1）求侧面PAD与底面ABCD所成的二面角的大小；
（2）若E是PB的中点，求异面直线PD与AE所成角的正切值；
（3）问在棱AD上是否存在一点F，使EF⊥侧面PBC，若存在，试确定点F的位置；若不存在，说明理由．
粤公网安备 44130202000953号