为了保证信息安全传输，设计一种密码系统，其加密、解密原理如下图：
现在加密方式为：把发送的数字信息X，写为“a11a21a12a22”的形式，先左乘矩阵A=
，再左乘矩阵B=
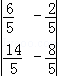，得到密文Y，现在已知接收方得到的密文4，12，36，72，试破解该密码．
中，
.
是数列中的第几项？
为何值时，
有最小值？并求最小值.
中，
，求
，并归纳出
.
中，
，求
的值.
，其中后一项比前一项大2.
是否为此数列的项？
中，
，求
，并归纳出
.推荐套卷
为了保证信息安全传输，设计一种密码系统，其加密、解密原理如下图：
现在加密方式为：把发送的数字信息X，写为“a11a21a12a22”的形式，先左乘矩阵A=，再左乘矩阵B=，得到密文Y，现在已知接收方得到的密文4，12，36，72，试破解该密码．
粤公网安备 44130202000953号