2014年国庆长假期间，各旅游景区人数发生“井喷”现象，给旅游区的管理提出了严峻的考验，国庆后，某旅游区管理部门对该区景点进一步改造升级，提高旅游增加值，经过市场调查，旅游增加值y万元与投入x万元之间满足：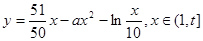
，当x＝10时，y＝9．2．
(1)求y＝f(x)的解析式;
(2)求旅游增加值y取得最大值时对应的x值．
求证：
满足
求证：
，求证：f（1）+f（2）+…+f（n）>n+
.
求证：
推荐套卷
2014年国庆长假期间，各旅游景区人数发生“井喷”现象，给旅游区的管理提出了严峻的考验，国庆后，某旅游区管理部门对该区景点进一步改造升级，提高旅游增加值，经过市场调查，旅游增加值y万元与投入x万元之间满足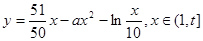：，当x＝10时，y＝9．2．
(1)求y＝f(x)的解析式;
(2)求旅游增加值y取得最大值时对应的x值．
粤公网安备 44130202000953号