(本题满分14分) 本题有2个小题，第一小题满分6分，第二小题满分8分。
如图，圆锥顶点为P，底面圆心为O，其母线与底面所成的角为22.5°，AB和CD是底面圆O上的两条平行的弦，轴OP与平面PCD所成的角为60°.
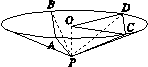
（1）证明：平面PAB与平面PCD的交线平行于底面；
（2）求cos∠COD.
中，底面
是正方形，侧棱
，
,
是
的中点，作
交
于点
．
；
．
的解集为
（1）求
中，
，
，
，
，
，求四边形
旋转一周所成几何体的表面积及体积.
和
.
与
交点坐标；
平行的直线方程。
满足
，若
，（1）求
的表达式；
时，求（1）中函数推荐套卷
(本题满分14分) 本题有2个小题，第一小题满分6分，第二小题满分8分。
如图，圆锥顶点为P，底面圆心为O，其母线与底面所成的角为22.5°，AB和CD是底面圆O上的两条平行的弦，轴OP与平面PCD所成的角为60°.
（1）证明：平面PAB与平面PCD的交线平行于底面；
（2）求cos∠COD.
粤公网安备 44130202000953号